【FPGA图像处理实战】- 双三次插值算法（放大和缩小）

本文将详细介绍缩放效果更好但计算量更大的双三次插值算法，包括算法基本原理、实现步骤、FPGA实现。

一、双三次插值算法

双三次插值（Bicubic interpolation）又叫双立方插值，是一种用于图像缩放的高阶插值方法，它通过在原始图像中选取16个像素点，并基于这些像素点进行加权平均来计算目标图像中每个像素的值。双三次插值算法可以生成较为平滑的缩放结果，但同时计算量也相对较大。

1、基本原理

遍历目标图像的每一个点，映射到原图像中，得到周围最近的16个点作为参考点，并根据权重计算函数计算权重系数，基于这个16个参考点，做水平方向和垂直方向的线性插值，也就是加权平均计算。

2、实现步骤

（1）映射坐标

根据图像的缩放比例，将目标图像中的每个像素点映射到原始图像中的相应位置。这个位置通常是一个浮点数坐标。设定（x,y）为目标图像中的一点，dstWidth和dstHeight为目标图像宽高，srcWidth和srcHeight是原图像的宽高，（fx,fy）是映射到原图像的浮点数坐标。

fx = x * ( srcWidth / dstWidth)，fy = y * ( srcHeight / dstHeight)

（2）找到邻近像素

在原始图像中找到与目标图像中每个像素点相对应的16个邻近像素点。这16个像素点分别位于目标像素点在原始图像中的周围。设定P点（fx,fy）为映射点浮点数坐标。

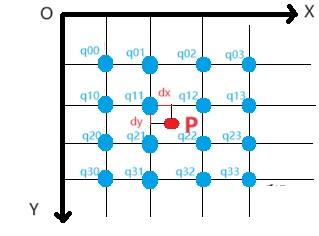
对这个浮点数坐标取整，则x = floor(fx)，y = floor(fy)，水平方向权重系数dx = fx - x，垂直方向权重系数dy = fy - y；那么参考的16个点坐标分别为q00 = (x-1, y-1)、q01 = (x, y-1)、q02 = (x+1, y-1) 、 q03 = (x+2, y-1)、q10 = (x-1, y)、q11 = (x, y)、q12 = (x+1, y) 、 q13 = (x+2, y)、q20 = (x-1, y+1)、q21 = (x, y+1)、q22 = (x+1, y+1) 、 q23 = (x+2, y+1)、q30 = (x-1, y+2)、q31 = (x, y+2)、q32 = (x+1, y+2) 、 q33 = (x+2, y+2)。

转换成矩阵计算公式：（W为权重计算函数，F为原图像坐标数据）

P（fx,fy） = A*B*C

A = { W(1 + dx), W(dx) , W(1 - dx), W(2 - dx)}

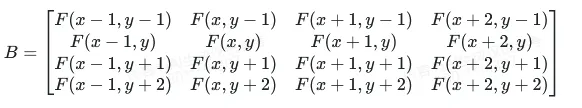
C = { W(1 + dy), W(dy) , W(1 - dy), W(2 - dy)}

（3）权重计算

每个像素点的权重是根据其距离映射点的距离来计算的，距离越近，权重越大。常用的插值计算权重函数有：Bicubic、Mitchell、Lanczos。

常用的Bicubic函数：x为目标像素点到附近点的距离，a值一般取1或-0.5。

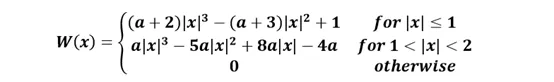
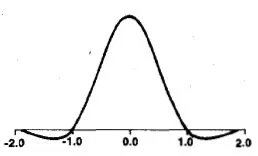
Lanczos核函数：

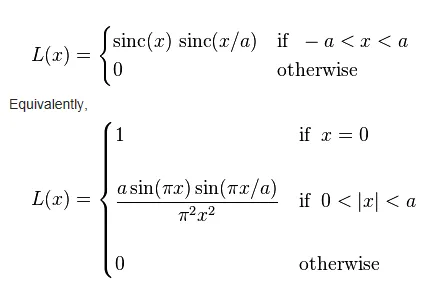
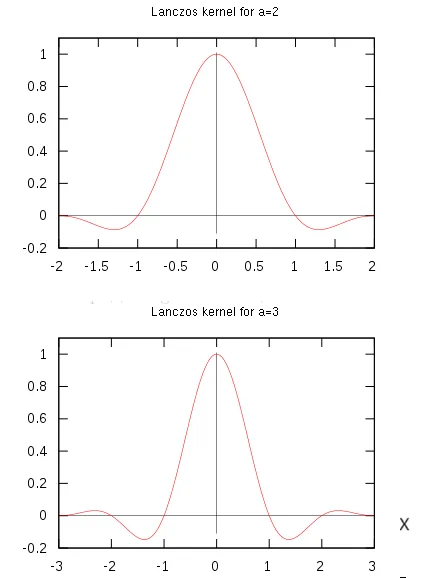
三角形采样：

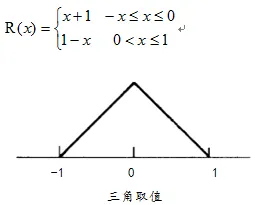
Bell分布采样：

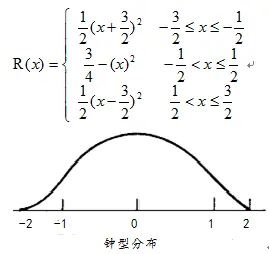
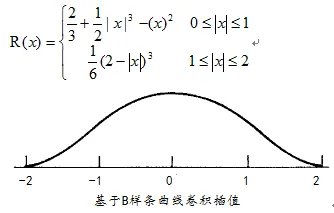
B样条曲线采样：

（4）水平方向插值

将16个参考点按照水平方向，分成4组：（q00、q01、q02、q03）、（q10、q11、q12、q13）、（q20、q21、q22、q23）和（q30、q31、q32、q33），分别进行加权平均计算，即为r0、r1、r2、r3、

r0 = W(1 + dx)*q00 + W(dx)*q01 + W(1 - dx)*q02 + W(2 - dx)*q03r1 = W(1 + dx)*q10 + W(dx)*q11 + W(1 - dx)*q12 + W(2 - dx)*q13r2 = W(1 + dx)*q20 + W(dx)*q21 + W(1 - dx)*q22 + W(2 - dx)*q23r3 = W(1 + dx)*q30 + W(dx)*q31 + W(1 - dx)*q32 + W(2 - dx)*q33

（5）垂直方向插值

按照垂直方向将r0、r1、r2、r3进行加权平均计算，得到像素点P最终的像素值。

P（fx,fy）= W(1 + dy)*r0 + W(dy)*r1 + W(1 - dy)*r2 + W(2 - dy)*r3

3、优点与缺点

（1）优点

双三次插值可以生成较为平滑的图像缩放结果，减少了锯齿现象。

可以较好地保持图像的细节和纹理信息。

（2）缺点

双三次插值的计算量较大，可能会对性能有一定的影响。

二、FPGA实现分析

缩放算法的基本结构都一样，主要分为2个部分：行数据缓存模块、插值算法计算模块（读数据地址逻辑、权重计算逻辑、插值数学运算）。

双三次插值算法的参考点是4*4窗口，所以行数据缓存模块需要缓存5行的乒乓模式。

与双线性插值算法相比，插值算法计算模块多了“权重计算逻辑”，且插值计算是4点加权平均计算。

如果需要工程源码，想要掌握更多的FPGA图像处理算法，学习FPGA图像算法的实现。请阅读下面这篇文章：

FPGA入门实战进阶专栏？看这里，少走弯路，少踩坑

FPGA图像处理入门基础系列文章汇总

注明：本内容来源网络，不用于商业使用，禁止转载，如有侵权，请来信到邮箱：429562386ⓐqq.com 或联系本站客服处理，感谢配合！